A simple way of assessing dispersion in models for count data
It has been some time since I have updated my blog, but I have plenty of good
excuses for justifying my lack of activity (or so I like to tell myself). In my post on simple models for abundance, I
introduced the Poisson-log GLM as the basic approach for
modelling count data. The Poisson-log GLM has an important limitation when it
comes to modelling ecological data: it assumes that the variance and the mean
of the response (dependent) variable are the same, so it is rather inflexible
for modelling response data with a variability exceeding the variation in the
mean. When this condition is not met, we obtain over- or under-dispersion in
the model. It is
important to note that the terms over- and under-dispersion do not refer to the
raw data values, but to the mean and variance expected with respect to a Poisson-log
GLM. It is a frequent mistake to think that dispersion refers to the raw
values of the response variable.
I should be more specific and technical when explaining what dispersion is: the dispersion in the Poisson-log GLM applies to the portion of the variability in the count data that cannot be accounted for by modelling the mean response as described in the post on modelling abundance. Therefore, dispersion refers to the residual (or conditional) mean and variance obtained after fitting a model. We talk about over- and under-dispersion in the response variable after the structure in the mean response has been accounted for with covariates. In summary, relative to the assumptions of a Poisson-log model, we classify dispersion as follows:
If residual
variance > residual mean: over-dispersion
If
residual variance < residual mean: under-dispersion
I have come to realise that over- and under-dispersion are very common in ecological models. In fact, I cannot recall the last time that I was
able to use a Poisson-log GLM for my research: almost always I do need to
account for over- or under-dispersion (more frequently for over-dispersion). The two most usual sources of over- and under-dispersion in ecological modelling are, at least in my own experience:
- The presence of abundant zeroes in the response variable
- Important covariates have not been included in the model
It seems to be quite common to assume over-dispersion whenever there are many zeroes in the response variable, but that is not necessarily right. Choosing the appropriate model is fundamental for obtaining reliable inferences about the system of interest, so it is important to be able to assess whether we need to account for over- or under-dispersion. There are a few ways for doing it, but perhaps the most simple is to fit a quasi-Poisson GLM. The quasi-Poisson GLM is basically a Poisson-log GLM that accounts for the dispersion in the dataset by estimating an additional parameter, the dispersion parameter ϕ. This extra parameter has a straightforward interpretation:
ϕ < 1: interpret as under-dispersion
ϕ = 1: interpret as residual variance equals residual mean
ϕ > 1: interpret as over-dispersion
As usual, I will illustrate the use of a quasi-Poisson
model through an example in R. We are going to model the abundance of the Cunningham’s skink (Egernia cunninghami) in the Mt Lofty Ranges (South Australia). The species is
rare and considered endangered in South Australia due to its restricted range. In this
example, we will model the abundance of the Cunningham's skink as a function of vegetation
cover, with the same values as in the post on modelling abundance of the
hunstman spider (to make comparisons easy).
 |
| An adult Cunningham's skink photographed on Cleland Conservation Park, South Australia |
Let’s get started by simulating some data
in R:
#### sample.size: number of plots surveyed for Cunningham’s
skink, n = 30
set.seed(1000)
sample.size<-30
#### Simulate vegetation cover data for the plots
from a Beta distribution
veg.cov<-rbeta(sample.size, 0.5,
0.5)
#### Now, let’s define the parameters of the
Poisson-log GLM relationship between the
#### Cunningham’s skink abundance
and the vegetation cover
intercept.sim=-2 ####
Intercept; slope.sim=3 #### Slope
#### Define the mean Cunningham’s skink abundance λi as
a function of the
#### vegetation cover
lambda<-exp(intercept.sim+slope.sim*veg.cov)
#### Now, we induce
under-dispersion in the response variable by defining the
#### dispersion
parameter ϕ being less than 1
phi<-0.4
#### Finally, obtain the Cunningham’s skink abundance in each and every plot by drawing
####
values from a Poisson distribution with mean λi and dispersion parameter ϕ
abundance<-rpois(sample.size, phi*lambda)
##### Let’s have a look at the
relationship between the Cunningham's skink abundance and the
#### vegetation cover
plot(abundance~veg.cov,
xlab="Vegetation cover (%)", ylab="Skink abundance",
pch=19, cex=3)
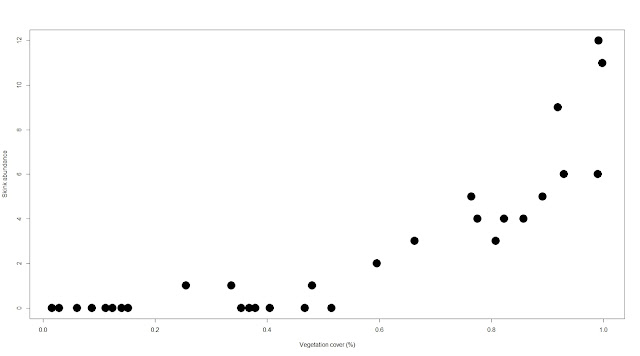 | |
|
Now, let's formally assess whether or not we have dispersion by using a quasi-Poisson GLM. Fitting a quasi-Poisson GLM
in R is as simple as it was fitting a Poisson-log GLM, and we only need one
line of code.
#### Fit a quasi-Poisson GLM to the Cunningham’s
skink abundance (response variable) and
#### vegetation cover data (independent covariate)
fit.ud<-glm(abundance~veg.cov,
family=quasipoisson())
#### Have a look at the summary Table
summary(fit.ud)
 | |
|
To assess dispersion, we have to pay attention to the estimated dispersion parameter
(highlighted in red). Remember the rules of thumb explained before for
interpreting the dispersion parameter – in this case, the estimate is 0.53 and we conclude that we have under-dispersion. Of course, there is
under-dispersion as we have simulated the dataset to be under-dispersed.
We can calculate the 95% confidence
intervals to see whether the estimates of the intercept and slope from the
quasi-Poisson model compare well to our simulated values. Interestingly, we see that our quasi-Poisson model recovers
#### Calculate the 95% confidence intervals
conf.int<-confint(fit.ud)
conf.int
 |
| 95% confidence intervals for the coefficients of the quasi-Poisson model |
Interestingly, we see that our quasi-Poisson model recovers the slope relatively well but that the intercept is not adequately recovered by the fitted model (the simulated value, -2, is not within the 95% CI). This result conveys an important message: you have to be cautious when presenting and interpreting results from models that account for over- and under-dispersion as the estimates might be biassed. Remember that the models that account for over- or under-dispersion need to estimate an additional parameter, implying that there is fewer data to estimate all the coefficients in the model (relative to a Poisson-log GLM). Fewer data relative to the number of coefficients to be estimated means higher chances of biassed and uncertain estimates.
This entry presented an example of how to evaluate the presence of over- or under-dispersion. There are other ways and tools for dealing with the added complication of dispersion. If you are interested in finding out more on the topic of modelling count data, I would recommend that you read the fantastic blog post by the UNSW Eco-Stats people and these two superb documents:
Zeileis et al. Regression models for count data in R
Potts & Elith. Comparing species abundance models
 |
| A close-up of two Cunningham's skinks on Morialta Conservation Park, South Australia |
The annotated R script for conducting the quasi-Poisson GLM can be found
in my GitHub repository: https://github.com/pablogarciadiaz/Code-Blog/blob/master/Code-Dispersion.R
No comments:
Post a Comment